Using electronvolts to measure mass
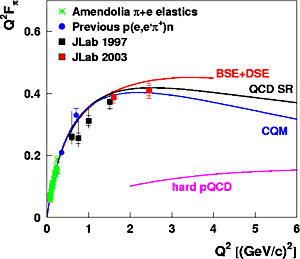
For comparison:

3.2×10 joule or 210 MeV - total energy released in fission of one Pu-239 atom (also on average)
Molecular bond energies are on the order of an electronvolt per molecule.
The typical atmospheric molecule has a kinetic energy of about 1/40 eV. This corresponds to room temperature. Electronvolts and energy
The energy E, frequency f, and wavelength λ of a photon are related by

where h is Planck's constant and c is the speed of light. For example, the spectrum of visible light consists of wavelengths ranging from 400 nm to 700 nm. Photons of visible light therefore have energies ranging from

to
.
An electronvolt is also the energy of an infrared photon with a wavelength of approximately 1240nm. 10eV would correspond to ultraviolet of 124nm, etc.

Electronvolts and photon properties
In particle physics, distances and times are sometimes expressed in inverse electronvolts via the conversion factors eV s
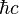= 197.326 960 2(77) eV nm Electronvolts and temperature