Compound interest is interest based not only on the original principal, but also on any unpaid interest that has been added to the principal. The more frequently interest is compounded, the faster the balance grows.
Interest rates must be comparable in order to be useful, and in order to be comparable, the interest rate and the compounding frequency must be disclosed. Since most people think of rates as a yearly percentage, many governments require financial institutions to disclose a (notionally) comparable yearly interest rate on deposits or advances. Compound interest rates may be referred to as Annual Percentage Rate, Effective interest rate, Effective Annual Rate, and by other terms. When a fee is charged up front to obtain a loan, APR usually counts that cost as well as the compound interest in converting to the equivalent rate. These government requirements assist consumers to more easily compare the actual cost of borrowing.Compound interest rates may be converted to allow for comparison: for any given interest rate and compounding frequency, an "equivalent" rate for a different compounding frequency exists.
Compound interest may be contrasted with simple interest, where interest is not added to the principal (there is no compounding). Compound interest predominates in finance and economics, and simple interest is used infrequently (although certain financial products may contain elements of simple interest).
Terminology
US and Canadian T-Bills (short term Government debt) have a different convention. Their interest is calculated as (100-P)/P where 'P' is the price paid. Instead of normalizing it to a year, the interest is prorated by the number of days 't': (365/t)*100. (See day count convention).
Corporate Bonds are most frequently payable twice yearly. The amount of interest paid (each six months) is the disclosed interest rate divided by two (multiplied by the principal). The yearly compounded rate is higher than the disclosed rate.
Canadian mortgage loans are generally semi-annual compounding with monthly (or more frequent) payments.
U.S. mortgages generally use monthly compounding (with corresponding payment periods).
Economists and certain techniques for, e.g., valuation of derivatives may use continuous compounding, where the maximum (bordering on infinite) frequency of compounding is used. Continuous compounding allows for the use of certain mathematical approaches that are more elegant and easier to compute. Exceptions
Mathematics of interest rates
Formulas are presented in greater detail at time value of money.
In the formulas below, i or r are the interest rate, expressed as a true percentage (i.e. 10% = 10/100 = 0.10). FV and PV represent the future and present value of a sum.
These are the most basic formulas required by a new student:
The above calculates the future value, (FV), of an investment, (PV), accruing at a fixed interest rate of i% for n periods. Also a=p(1+r/t)^nt can be used.
The above calculates what present value (PV) would be needed to produce a certain future value (FV) if interest of i% accrues for n periods.
The above two formulas are the same and calculate the compound interest rate i% achieved if an initial investment of PV returns a value of FV after n accrual periods.
Simple Formulas
Each time unpaid interest is compounded and added to the principal, the resulting principal is grossed up to equal P(1+i%).
A) You are told the interest is 8% a year, with 2%(=8/4) interest charged every quarter. What is the equivalent annual rate?. Start with $100. At the end of one year it will be: $100 (1+ .02) (1+ .02) (1+ .02) (1+ .02) = $108.24 We know that $100 invested at 8.24% will give you $108.24 at year end. So the equivalent rate is 8.24%. Using a financial calculator or a [table] is simpler still. Using the Future Value of a currency function, input
B) You know the equivalent annual interest rate is 4%, but it will be compounded quarterly. You need to find the interest rate that will be applied each quarter. $100 (1+ .009853) (1+ .009853) (1+ .009853) (1+ .009853) = $104 The mathematics to find the 0.9853% is discussed at Time value of money, but using a financial calculator or [table] is easier. Input
C) You sold your house for a 60% profit. What was the annual return? You owned the house for 4 years, paid $100,000 originally, and sold it for $160,000. $100,000 (1+ .1247) (1+ .1247) (1+ .1247) (1+ .1247) = $160,000 Find the 12.47% annual rate the same way as B.) above, using a financial calculator or [table]. Input
PV = 100
n = 4
i = .02
solve for FV = 108.24
PV = 100
n = 4
FV = 104
solve for interest = 0.9853%
PV = 100,000
n = 4
FV = 160,000
solve for interest = 12.47% Translating different compounding periods
In January 1970 the S&P 500 index stood at 92.06 and in January 2006 the index stood at 1248.29. What has been the annual rate of return achieved? (ignoring dividends).
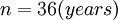
Example question:
Answer:
The Rule of 72 is a very simple way of illustrating the growth potential of compound interest. The rule says simply this:
, where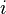 
is the interest rate and 
is the number of time periods needed to double the principal.For example, say a mutual fund grows at 12% average interest rate. According to the rule of 72, if money were invested in this mutual fund, then it would double every 6
years. This calculation deals only with the gross amount, taxes must be factored into growth if taxable vehicles (such as CD's, mutual funds, etc) are used.However, the above Rule of 72 merely gives an approximation of the time needed to retain an investment before it doubles in value. The accurate calculation is as follows:
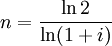
The Rule of 72
The amount function for compound interest is an exponential function in terms of time.
As n increases, the rate approaches an upper limit of e. This rate is called continuous compounding, see below.
Since the principal A(0) is simply a coefficient, it is often dropped for simplicity, and the resulting accumulation function is used in interest theory instead. Accumulation functions for simple and compound interest are listed below:
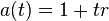
Note: A(t) is the amount function and a(t) is the accumulation function.
n = Number of compounding periods per each t (time in years) (note that the total number of compounding periods is
)r = Nominal annual interest rate expressed as a decimal. e.g.: 6% = 0.06 Periodic compounding
In mathematics, the accumulation functions are often expressed in terms of e, the base of the natural logarithm. This facilitates the use of calculus methods in manipulation of interest formulas. This is called the force of interest.
The force of interest is defined as the following:
. Note that this equation contains an ERROR given the previous equation. The below is a deemed correction.
When the above formula is written in differential equation format, the force of interest is simply the coefficient of amount of change.
The force of interest for compound interest is a constant for a given r, and the accumulation function of compounding interest in terms of force of interest is a simple power of e:
Continuous compounding
See Day count convention
To convert an interest rate from one compounding basis to another compounding basis, the following formula applies:
where r1 is the stated interest rate with compounding frequency n1 and r2 is the stated interest rate with compounding frequency n2.When interest is continuously compounded:
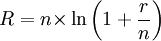
where R is the interest rate on a continuous compounding basis and r is the stated interest rate with a compounding frequency n.
Another formula to calculate compound interest is
where y is the money after interest is calculated, a is the initial deposit, b is the interest rate in a decimal form (divided by the number of compoundings if applicable), and x is the exponent of b which represents the time (multiplied by the number of compoundings if applicable).History
Effective interest rate
Nominal interest rate
Exponential growth
Rate of return on investment
Credit card interest
Fisher equation
Yield curve
No comments:
Post a Comment